Preface
As an important part of advanced manufacturing technology, the development of welding technology in the future will move from "technique" to "scientific", and the development of welding process simulation technology is an important symbol. Since Rosenthal's mobile heat source solid heat conduction model and the analytical solution for establishing the welding temperature field, many welding workers have worked hard to study the computer simulation technology of the welding process. For example, Ueda Ueda first analyzed the stress and strain of the welding process using finite element technology.
At present, the simulation objects in the field of welding mainly include temperature, displacement, strain, stress and the like. What really affects the overall structural performance is stress and strain, which is the ultimate object of the simulation. However, stress and strain are more difficult to test (the existing detection methods are mostly not resistant to high temperature or destructive), so from the perspective of whether it is suitable for the result verification, the displacement field should be used as the direct analog quantity. After the correctness of the simulation is verified, the stress strain results are derived for analysis.
1 Establishment of constitutive equation
The establishment of constitutive relations is closely related to the state of materials. The metal component of the welding process has to go through two stages: heating and cooling. At a certain moment, there will be a solid phase zone, a liquid phase zone and a solid-liquid coexistence zone on the component, which affects the equations used in the calculation. The solid-liquid coexistence zone has great viscosity and conforms to viscoelastic-plastic finite element. However, due to the fast cooling rate under welding conditions, the solid-liquid zone has a short time and can be neglected. Therefore, the solid phase zone and the liquid phase zone are mainly considered. The stress and strain in the solid state obey the thermal elastoplastic theory. The material properties of the material are temperature-dependent thermoelastic-plastic incremental stress-strain relationship, which is derived from the isotropically strengthened Von Mises yield criterion and the Prandtl-Reuss flow increment theory. The equation is as shown in Equation 1.
d{σ}=[D]d{ε}-{C}dT (1)
In the formula: 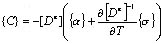
[D]: elastoplastic matrix, in the elastic region [D]=[De],
In the plastic zone [D]=[D]ep=[De]-[D]p
Where [De]: elastic matrix [D]ep-elastoplastic matrix {α}-linear expansion coefficient vector For thermal elastoplasticity, its detailed expansion is: 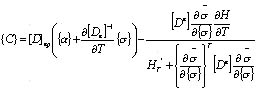
Where H: strain hardening index T: equivalent stress according to the principle of virtual displacement, the incremental expression of the finite element equation is established as shown in Equation 3.
[K]e△{δ}=△{R}e (3)
Where: [K]e: element stiffness matrix [K]e=∫∫e[B]T[D][B]dxdy
{δ}: displacement increment caused by this loading (or temperature increment) {R}e: unit equivalent nodal force vector △{R}e=∫∫e[B]T{C}△Tdxdy
The above is obtained under certain theoretical assumptions, the hypothesis is as follows: the behavior in the plastic zone obeys the flow rule and shows strain hardening; the elastic strain, the plastic strain and the temperature strain are separable; the mechanical properties of the material vary with temperature. ; does not consider the effects of viscosity and creep; material isotropic.
Next page
Flat Washers,Stainless Steel Shim Rings,Ring Shim Washers,Stainless Steel Shim Washers
Kunshan Liyue Hardware Products Co.,Ltd , https://www.fixlyhardware.com